kuis KSK Desi rose algoritma

Kriptografi secara cepat telah menjadi sebuah bagian yang sangat krusial dalam dunia ekonomi. Sebelum tahun 1980-an, kriptografi digunakan utamanya untuk bidang militer dan komunikasi diplomatik, dan hampir dalam kontekskonteks yang dibatasi. Dalam dunia belakangan ini, komunikasi berkembang dengan sangat cepatdengan adanya   Faktanya kriptologi telah sangat bertambah luas, dari studi tentang sandi rahasia menjadi studi tentang kemanan informasi. Algoritma penyandian data yang telah dijadikan standar sejak tahun 1977 adalah Data Encryption Standard (DES). Kekuatan
teknologi internet, akibatnya seorang hacker dengan siap sedia bisa mengintip transmisi data komputer untuk informasi yang berharga. Sekarang kita harus bisa melindungi cara akses kita ke komputer (melalui sandi lewat (password) dan akses jarak jauh yang terenkripsi), transaksi komersial kita (nomor-nomor kartu kredit dan data bank), data medis kita (yang sebentar lagi akan disimpan dalam sebuah kartu cerdas (smart card)), dan informasiinformasi lainnya.

DES ini terletak pada panjang kuncinya yaitu 56-bit. Perkembangan kecepatan perangkat keras dan meluasnya penggunaan jaringan komputer terdistribusi mengakibatkan penggunaan DES, dalam beberapa hal, terbukti sudah tidak aman dan tidak mencukupi lagi terutama dalam hal yang pengiriman data melalui jaringan internet. Perangkat keras khusus yang bertujuan untuk menentukan kunci 56-bit DES hanya dalam waktu beberapa jam sudah dapat dibangun. Beberapa pertimbangan tersebut telah manandakan bahwa diperlukan sebuah standar algoritma baru dan kunci yang lebih panjang.  Untuk menyandi informasi dan untuk menterjemahkan pesan tersandi sebuah algoritma penyandian memerlukan sebuah data binar yang disebut kunci. Tanpa kunci yang cocok orang tidak bisa mendapatkan kembali pesan asli dari pesan tersandi. Pada DES digunakan kunci yang sama untuk menyandi (enkripsi) maupun untuk menterjemahan (dekripsi), sedangkan RSA (algoritma kriptografi yang diciptakan Ron Rivest, Adi Sharmir, dan Len Adleman) menggunakan dua kunci yang berbeda.

Isitilahnya, DES disebut sistem sandi simetris sementara RSA disebut sistem sandi asimetris.  Kedua sistem ini memiliki keuntungan dan kerugiannya sendiri. Sistem sandi simetris cenderung jauh lebih cepat sehingga lebih disukai oleh sementara kalangan industri. Kejelekannya, pihakpihak yang ingin berkomunikasi secara privat harus punya akses ke sebuah kunci DES bersama. Walaupun bisaanya pihak-pihak yang terkait sudah saling percaya, skema ini memungkinkan satu pihak untuk memalsukan pernyataan dari pihak lainnya. Contoh, Agus dan Fatma menggunakan DES untuk melindungi komunikasi privat mereka. Untuk itu mereka menyetujui sebuah kunci DES yang dipakai bersama. Suatu saat Agus mengirim sebuah pesan tersandi untuk Fatma bahwa ia akan menjamin semua hutang Fatma.  Seminggu kemudian Fatma betul-betul membutuhkan jaminan Agus. Akan tetapi Agus mungkir dan bahkan menuduh Fatma melakukan pemalsuan. Fatma tidak bisa berbuat apa-apa karena tidak bisa membuktikan bahwa Agus berbohong (dan sebaliknya Agus juga tidak bisa membuktikan pemalsuan Fatma, kalau itu yang terjadi). Ini terjadi karena Fatma dan Agus berbagi kunci yang sama. Jadi, keduanya sama-sama bisa ‘merekayasa’ surat jaminan Agus tadi. Kalau kita lihat dalam dunia nonelektronis, dokumen-dokumen sering ada tanda tangannya, atau cap organisasi. Tanda tangan dan cap tersebut ditujukan untuk meyakinkan penerima dokumen bahwa dokumen tersebut memang asli berasal dari individu atau organisasi yang tandatangan/capnya tertera di dokumen tersebut.  Mekanisme serupa tentunya juga dibutuhkan oleh dokumen-dokumen elektronis (disebut sertifikat/tanda-tangan digital). Dari cerita Fatma dan Agus diatas kita lihat bahwa yang dibutuhkan adalah mekanisme tanda tangan digital. Sekarang Fatma hanya akan mempercayai pernyataan Agus kalau pernyataan tersebut dilengkapi oleh tanda-tangan digital Agus, karena dengan itu Agus nantinya tidak bisa mungkir lagi. Sistem sandi asimetris seperti RSA bisa juga digunakan sebagai tanda tangan digital. Ini membuat aplikasi yang bisa dibuat menggunakan sistem sandi asimetris jauh lebih banyak.  Sebagai contoh uang digital tidak bisa dibuat tanpa menggunakan sistem sandi asimetris. Protokol e-commerce seperti SET juga tidak bisa dibuat tanpa sistem sandi ini. Untuk mendapatkan keuntungan yang optimal orang pada prakteknya menggabungkan sistem sandi asimetris dengan yang simetris, seperti yang dilakukan Zimmermann dalam sandi publicdomain-nya yaitu PGP (Prety Good Privacy). Saat ini satu-satunya cara yang diketahui untuk mendobrak sandi DES dan RSA adalah dengan mencoba satu per satu berbagai kombinasi kunci (istilahnya: brute force attack). Karena itu keamanan dari DES dan RSA banyak bergantung dari ukuran

kunci yang digunakan (dalam bit). Ukuran tersebut menentukan jumlah kombinasi kunci yang mungkin. DES menggunakan ukuran kunci 56 bit sehingga total banyaknya kombinasi kunci yang mungkin adalah 256. Jumlah ini sangat besar. Untuk membongkar sandi tersebut dengan menggunakan PC Pentium yang berkemampuan mengerjakan 200 juta operasi per detik kita masih membutuhkan 5 tahun. Dengan mesin yang lebih baik orang bisa melakukannya lebih cepat, tetapi biayanya juga menjadi mahal. Ini membuat usaha pembongkaran seperti itu menjadi tidak ekonomis. Standar industri saat ini bahkan menggunakan Triple DES yang ukuran kuncinya 112 bit. Ini membuat usaha untuk mendobrak sandi ini dengan brute force menjadi 1016 kali lebih sulit! Untuk RSA, panjang kuncinya bisa diatur. Misalnya ukuran kunci RSA yang digunakan oleh modul sekuriti browser Netscape Anda ukurannya 48 bit. Ukuran ini sudah tidak aman lagi sekarang, tetapi pemerintah AS memang melarang ekspor produk-produk RSA yang menggunakan kunci lebih besar dari 48 bit.  Standar saat ini merekomendasikan ukuran 512 bit (walaupun hukum Termodinamika menunjukkan bahwa 256 bit saja sudah terlalu sulit untuk dibrute-force-attack oleh computer apapun selama komputer itu terbuat dari materi). Saat ini juga, seperti telah menjadi suatu kesepakatan profesi yang tidak tertulis, yaitu tugas para ahli kriptografi adalah menemukan suatu sistem sandi yang sulit dipecahkan, sedangkan tugas para hacker adalah menemukan kelemahan pada sistem sandi itu. Secara khusus, dalam makalah ini penulis akan mencoba membahas tentang algoritma RSA dan perkembangannya. RSA telah menjadi bahan pembicaraan yang sangat populer dalam dunia keamanan informasi saat ini. Dalam situs resmi RSA (http://www. rsasecurity. com) bahkan telah dilombakan beberapa kode RSA yang jika bisa ditebak dengan benar, maka akan dihadiahkan sejumlah uang. RSA sejauh ini merupakan algoritma kriptografi yang paling sering digunakan karena sangat sulit untuk dipecahkan. Sejauh ini belum seorang pun yang berhasil menemukan lubang sekuriti pada RSA, tetapi tak seorang pun juga berhasil memberikan pembuktian ilmiah yang memuaskan dari keamanan teknik sandi ini. Padahal, pemakaiannya sudah sangat meluas dan mencakup sektor-sektor strategis seperti perbankan dan pemerintahan. 

2.  Algoritma RSA Dalam kriptografi, RSA adalah algoritma untuk enkripsi kunci publik (public-key encryption). Algoritma ini adalah algoritma pertama yang diketahui paling cocok untuk menandai (signing) dan untuk enkripsi (encryption) dan salah satu penemuan besar pertama dalam kriptografi kunci publik. RSA masih digunakan secara luas dalam protokol-protokol

perdagangan elektronik, dan dipercayai sangat aman karena diberikan  kunci-kunci yang cukup panjang dan penerapanpenerapannya yang sangat up-to-date (mutakhir). 

2.1.  Sejarah RSA Algortima RSA dijabarkan pada tahun 1977 oleh Ron Rivest, Adi Shamir dan Len Adleman dari MIT. Huruf RSA itu sendiri juga berasal dari inisial nama mereka (Rivest—Shamir— Adleman). Clifford Cocks, seorang matematikawan Inggris yang bekerja untuk GCHQ, menjabarkan tentang sistem equivalen pada dokumen internal di tahun 1973. Penemuan Clifford Cocks tidak terungkap hingga tahun 1997 dikarenan alasan top-secret classification. Algoritma tersebut dipatenkan oleh Massachusetts Institute of Technology pada tahun 1983 di Amerika Serikat sebagai U. S. Patent 4405829.  Paten tersebut berlaku hingga 21 September 2000. Semenjak Algoritma RSA dipublikasikan sebagai aplikasi paten, regulasi di sebagian besar negara-negara lain tidak memungkinkan penggunaan paten. Hal ini menyebabkan hasil temuan Clifford Cocks di kenal secara umum, paten di Amerika Serikat tidak dapat mematenkannya. 

2.2. Membuat Kunci Privat (Private Key) dan Kunci Publik (Public Key) Berikut ini langkah-langkahnya adalah: 1. Pilih dua buah bilangan prima sembarang, sebut a dan b. Jaga kerahasiaan a dan b ini. 2. Hitung n = a x b. Besaran n tidak dirahasiakan.  3. Hitung m = (a - 1) x (b - 1). Sekali m dapat dihitung, a dan b dapat dihapus untuk mencegah diketahuinya oleh orang lain. 4. Pilih sebuah bilangan bulat untuk kunci publik, sebut namanya e, yang relatif prima terhadap m.  5. Bangkitkan kunci dekripsi, d, dengan kekongruenan ed ≡ 1(mod m). Lakukan enkripsi terhadap isi pesan dengan persamaan ci = pie mod n, yang dalam hal ini pi adalah blok plainteks, ci adalah chiperteks yang diperoleh, dan e adalah kunci enkripsi (kunci publik). Harus dipenuhi persyaratan bahwa nilai pi harus terletak dalam himpunan nilai 0, 1, 2, . . . , n – 1 untuk menjamin hasil perhitungan tidak berada di luar himpunan.  6. Proses dekripsi dilakukan dengan menggunakan persamaan pi = cid mod n, yang dalam hal ini d adalah kunci dekripsi (kunci privat). Perhatikan pada langkah 4, kekongruenan ed ≡ 1(mod m) sama dengan ed mod m = 1. Menurut persamaan Chinese RemainderTheorem (CRT) yang menyatakan bahwa a ≡ b (mod m) ekivalen dengan a = b + km, maka ed ≡ 1(mod m) ekivalen dengan ed = 1 + km, sehingga d dapat dihitung dengan:

Akan terdapat bilangan bulat k yang menyebabkan (1.1) memberikan bilangan bulat d. 

Berikut ini adalah contoh untuk kasus dengan nilai a dan b yang kecil. Sebagai ilustrasi, marilah kita mengambil a = 47 dan b = 71 (keduanya prima), maka dapat dihitung nilai n = a x b = 3337 dan m = (a - 1)x(b - 1) = 3220. Pilih kunci publik e = 79 (relatif prima terhadap 3220 karena pembagi terbesarnya adalah 1). Nilai e dan m dapat dipublikasikan ke umum. Selanjutnya akan dihitung kunci dekripsi d seperti yang dituliskan pada langkah instruksi 4. 

e x d ≡1 (mod m)

Dengan menggunakan (1.1) kita menghitung kunci dekripsi d sebagai berikut:

Dengan mencoba nilai-nilai k = 1, 2, 3, . . . , diperoleh nilai d yang bulat adalah 1019. Ini adalah kunci deskripsi yang harus dirahasiakan Misalkan plainteks yang akan dienkripsikan adalah p = “HARI INI” (atau dalam decimal ASCII-nya adalah 7265827332737873). Pecah p menjadi blok-blok yang lebih kecil, misalnya p dipecah menjadi enam blok yang berukuran 3 digit : p1 = 726, p2 = 582, p3 = 733, p4 = 273, p5 = 787, dan p6 = 003. Nilai-nilai pi ini masih terletak dalam rentang 0 sampai 3337 – 1. Blok pertama dienkripsikan sebagai 72679 mod 3337 = 215 = c1. Blok kedua dienkripsikan sebagai 58279 mod 3337 = 776 = c2. Dengan melakukan proses yang sama untuk sisa blok lainnya, dihasilkan chiperteks C 215 776 1743 933 1731 158. Proses dekripsi dilakukan dengan menggunakan kunci privat d = 1019, jadi blok c1 didekripsikan sebagai 2151019 mod 3337 = 726 = p1 , blok c2 didekripsikan sebagai 7761019 mod 3337 = 582 = p2. Blok plainteks yang lain dikembalikan dengan cara yang serupa. Akhirnya kita memperoleh kembali plainteks semula p = 7265827332737873 yang karakternya adalah p = “HARI INI”. Perhitungan perpangkatan pada proses enkripsi (ci = pie mod n) dan dekripsi (pi = cid mod n) membutuhkan bilangan yang sangat besar. Untuk menghindari penggunaan bilangan yang sangat besar, maka dapat digunakan penyederhanaan

dengan persamaan berikut : ab mod m = [(a mod m) (b mod m)] mod m. 

3.  Kecepatan Algoritma RSA Sebuah operasi RSA, baik enkripsi, dekripsi, penandaan, atau verifikasi intinya adalah sebuah eksponensial terhadap modul. Proses perhitungan ini ditunjukkan oleh sebuah rangkaian dari multiplikasi terhadap modul. Dalam aplikasi praktikal, adalah umum untuk menentukan sebuah eksponen kecil yang umum sebagai kunci public. Faktanya, keseluruhan kelompok dari user (pemakai) bisa memakai eksponen yang sama, dengan berbeda modulus. (Terdapat beberapa pembatasan pada faktorfaktor prima dari eksponen publik ketika diputuskan.)  Hal ini menyebabkan proses enkripsi lebih cepat daripada proses dekripsi dan verifikasi lebih cepat dari pada penandaan. Dengan algoritma eksponensial modular (modular exponentiation) yang khas yang digunakan untuk mengimplementasikan algoritma RSA, operasi kunci public membutuhkan O(k2) langkah, operasi kunci privat membutuhkan O(k3) langkah, pembangitan kunci membutuhkan O(k4) langkah, di mana k adalah jumlah bit dari modulus. Teknik multiplikasi cepat, seperti metode pada Fast Fourier Transform (FFT), membutuhkan langkah-langkah yang lebih sedikit secara asimtotik.  Dalam praktiknya, hal di atas tidaklah umum melihat pada kompleksitas perangkat lunak yang lebih besar dan kenyataan bahwa mungkin akan lebih lambat untuk beberapa ukuran kunci yang khas. Sebagai perbandingan, algoritma DES dan beberapa chiper blok yang lain jauh lebih cepat bdaripada algoritma RSA. DES secara umum 100 kali lebih cepat pada perangkat lunak dan antara 1. 000 dan 10. 000 kali lebih cepat pada perangkat keras, tergantung dari implementasinya. Implementasi dari algoritma RSA mungkin akan mempersempit celah beberapa bit dalam tahuntahun mendatang, melihat tingginya permintaan, tapi bagaimana pun juga, chiper blok akan bertambah lebih cepat. 

4.  Panjang Kunci yang Aman Ukuran kunci dalam algoritma RSA menunjuk kepada ukuran dari modulus n. Dua bilangan prima, p dan q, yang membentuk modulus, kirakira harus memiliki panjang yang sama; hal ini menyebabkan modulus ini akan lebih sulit untuk difaktorkan dibandingkan apabila salah satu dari bilangan prima tersebut jauh lebih kecil dari yang lainnya. Jika seseorang memilih untuk menggunakan modulus 768 bit, bilangan primanya harus memiliki panjang kira-kira 384 bit. Jika kedua bilangan prima tersebut sangat dekat atau perbedaannya dekat dengan suatu bilangan yang telah ditentukan sebelumnya.   Selalu ada potensi resiko keamanan, tetapi kemungkinan bahwa kedua bilangan prima acak yang dipilih sangat dekat dapat diabaikan. Ukuran terbaik

untuk untuk sebuah modulus tergantung pada kebutuhan keamanannya sendiri. Semakin besar modulus, semakin besar tingkat keamanannya, tetapi juga semakin lambat operasi alogoritma RSA-nya. Seseorang ketika memilih suatu kunci harus dengan pertimbangan, pertama, nilai dari data yang dilindungi dan berapa lama data tersebut butuh dilindungi, dan, kedua, seberapa kuat suatu potensi ancaman mungkin terjadi. Pada tahun 1997, sebuah taksiran terhadap keamanan kunci RSA 512 bit menunjukkan bahwa untuk memfaktorkannya dibutuhkan dana lebih dari $1,000,000 dan waktu lebih dari delapan bulan. Kenyataannya, angka RSA155 512 bit difaktorkan dalam tujuh bulan selama 1999. Hal ini berarti kunci 512 bit tidak lagi menyediakan keamanan yang cukup untuk keamanan yang lebih dari kebutuhan keamanan jangka pendek. Lebih dianjurkan untuk menggunakan ukuran kunci 1024 bit untuk hal yang berhubungan dengan hukum dan 2048 bit untuk kunci-kunci yang ekstrem, seperti kunci yang digunakan oleh alat untuk verfikasi wewenang. Beberapa standar pada saat ini lebih menganjurkan 1024 bit untuk penggunaan dalam bidang hukum. Informasi yang lebih tidak terlalu penting sudah cukup dienkripsi dengan kunci 768 bit.  Bisaanya harus dipastikan bahwa sebuah kunci untuk perseorangan habis masa berlakunya setelah jangka waktu yang pasti, katakanlah, dua tahun. Hal ini memberikan kesempatan agar kunci dapat diubah secara teratur dan mempertahankan level keamanan yang diberikan. Setelah habis masa berlakunya, seorang user harus membangkitkan kuncinya yang baru untuk menegaskan apakah terdapat perubahan dalam panjang kunci yang dibutuhkan. Tentu saja, mengganti kunci bukanlah bertahan dari serangan yang berusaha untuk mendapatkan kembali pesan yang dienkripsi dengan kunci lama, jadi ukuran kunci selalu harus dipilih merujuk pada waktu penggunaan data yang diinginkan.  Kesempatan untuk mengubah  kunci-kunci memperbolehkan seseorang untuk membisaakan diri dengan rekomendasi panjang kunci yang baru. User harus selalu berpendapat bahwa waktu yang diperlukan untuk memecahkan sistem RSA hanyalah rata-rata. Suatu usaha penyerangan yang besar, menyerang ribuan modul, mungkin berhasil minimal satu modul dalam waktu yang layak. Walaupun keamanan dari suatu kunci perseoarangan masih kuat, dengan beberapa metode pemfaktoran selalu ada kemungkinan kecil seorang penyerang mungkin beruntung dan dapat memfaktorkan suatu kunci dengan cepat.  Melipatduakan panjang dari modulus akan, secara rata-rata, meningkatkan waktu yang dibutuhkan untuk operasi kunci publik (enkripsi dan verifikasi tanda) dengan kelipatan empat, dan meningkatkan waktu untuk operasi kunci privat (dekripsi dan penandaan) dengan kelipatan delapan.

Kunci publik lebih sedikit dipengaruhi daripada kunci privat karena eksponen public bisa tetap ketika modulus ditingkatkan, sedangkan panjang eksponen privat meningkat per bagian. Waktu untuk pembangkitan kunci akan meningkat dengan kelipatan 16 untuk setiap pe-lipatdua-an modulus, tetapi hal ini merupakan operasi yang relatif jarang bagi user. Juga harus diperhatikan ukuran kunci untuk sistem RSA (dan teknik kunci publik lainnya) jauh lebih besar daripada ukuran kunci untuk chiper blok seperti DES, tetapi keamanan dari kunci RSA tidak bisa dibandingkan dengan tingkat keamanan kunci dari sistem yang lainnya dalam beberapa jangka waktu. 

5. Memecahkan Kode RSA Ada beberapa interpretasi yang mungkin dari memecahkan sistem RSA. Yang paling merusakkan adalah seorang penyerang yang menemukan kunci privat yang berkorespondensi dengan sebuah kunci publik yang disebarluaskan. Hal ini akan membuat sang penyerang bisa membaca semua pesan yang terenksripsi dengan kunci public dan memalsukan tanda.  Cara yang paling jelas untuk melakukan serangan jenis ini adalah dengan memfaktorkan modulus publik, n , ke dalam dua buah faktor prima, p dan q. Dari p, q, dan e, publik eksponen, sang penyerang bisa secara mudah mendapatkan d, eksponen privat. Hal yang paling sulit adalah memfaktorkan n. Keamanan RSA tergantung pada kesulitan dalam memfaktorkan n. Dalam dunia nyata, pekerjaan memperoleh kunci privat sama dengan pekerjaan mencari faktor dari modulus, yaitu menggunakan d untuk memfaktorkan n, sama dengan menggunakan faktorisasi dari n untuk mendapatkan d.  Hal yang harus dicatat lainnya, perkembangan perangkat lunak saja tidak akan membuat algoritma RSA menjadi lemah, selama digunakan panjang kunci yang sesuai. Faktanya, perkembangan perangkat keras menaikkan keamanan dari suatu sistem kriptografi.  Cara lain untuk memcahkan algoritma RSA adalah dengan menemukan sebuah teknik untuk menghitung akar ke-e mod n. Karena c = me mod n , akar ke-e dari c mod n adalah pesan m. Serangan ini akan memperbolehkan seseorang memperoleh kembali pesan-pesan yang telah terenkipsi dan memalsukan tanda, bahkan tanpa mengetahui kunci privat. Serangan jenis ini tidak sama dengan memfaktorkan. Tidak ada metode umum yang sekarang sekarang dikenali mencoba untuk memcahkan sistem RSA dengan cara ini. Bagaimanapun juga, dalam beberapa kasus khusus di mana pesan-pesan yang saling berhubungan dan diperbanyak dienkripsi dengan eksponen kecil yang sama, mungkin terjadi pesan diperoleh kembali. Hanya beberapa serangan yang baru saja disebutkan

di ataslah cara untuk memecahkan sistem RSA untuk mendapatkan kembali pesan terenkripsi tanpa kunci privat. Terdapat beberapa mtode lain, bagaimanapun juga, yang bertujuan untuk mendapatkan kembali pesan-pesan tunggal. Beberapa orang bahkan mempelajari secara khusus apakah bagian dari pesan bisa diperoleh kembali dari sebuah pesan terenkripsi.  Cara menyerang pesan tunggal yang paling sederhana adalah dengan serangan menebak plainteks. Seorang penyerang mengamati sebuah chiperteks dan menebak apa sebenarnya pesan tersebut, sebagai contoh, ”Serang pada fajar”, dan mengenkripsi tebakan ini dengan suatu kunci publik dari sang penerima dan dengan membandingkan dengan chiperteks, sang penyerang akan bisa mengetahui apakah tebakannya benar. Menambahkan beberapa bit acak pada pesan dapat menghalangi serangan jenis ini. Serangan pesan tunggal yang lainnya bisa terjadi jika seseorang mengirimkan m pesan yang sama kepada tiga orang lain, dimana setiap orang memiliki kunci publik e = 3.  Seorang penyerang yang mengetahui tentang hal ini dan melihat ketiga pesan akan dapat mendapatkan kembali pesan m. Sayangnya, serangan jenis ini juga bisa dikalahkan dengan melapisi pesan sebelum enkripsi dengan beberapa bit acak. Terdapat juga beberapa serangan chiperteks yang dipilih (atau serangan pesan yang dipilih untuk mengubah pesan), di mana sang penyerang menciptakan suatu chiperteks dan melihat pada plainteks yang berkorespondensi, barangkali dengan menipu user yang sah untuk mendekripsi sebuah pesan yang palsu. Tentu saja, terdapat juga beberapa serangan yang tujuannya bukan sistem kriptografi tetapi pada implementasi sistem yang tidak kokoh.  Serangan jenis ini tidak digolongkan sebagai pemecahan sistem RSA, karena bukan kelemahan dari algoritma RSA yang dimanfaatkan, tetapi lebih kepada kelemahan dalam implementasi yang spesifik. Contohnya, bila seseorang menyimpan kunci privat dengan tidak aman, seorang penyerang mungkin menermukannya. Sistem RSA membutuhkan sebuah implementasi yang aman. Ukuran matematika untuk keamanan, seperti memilih ukuran kunci yang panjang, tidaklah cukup. Pada kenyataannya, beberapa serangan yang berhasil menyerang implementasi yang tidak aman dan tingkatan pengelolaan kunci dari sebuah sistem RSA. 

6.  Contoh Kasus Algoritma RSA Untuk Pribadi Dalam Praktiknya Pada praktiknya, sistem RSA sering digunakan bersama-sama dengan sistem kriptografi dengan kunci rahasia, seperti DES, untuk mengenkripsi sebuah pesan dengan jenis sebuah amplop digital RSA. Umpamanya Fatma hendak mengirimkan sebuah pesan yang terenkripsi kepada Agus. Pertama dia mengenkripsi pesan tersebut dengan DES, menggunakan kunci acak DES yang

telah dipilih. Kemudian Fatma menggunakan kunci public RSA Agus untuk mengenkripsi kunci DES. Pesan DES yang telah terenkripsi dan kunci DES yang telah terenkripsi dengan RSA disatukan dalam bentuk amplop digital RSA dan dikirimkan kepada Agus. Setelah menerima amplop digital, Agus mengdekripsikan kunci DES dengan kunci privat miliknya, barulah menggunakan kuci DES untuk mengdekripsikan pesan itu sendiri. Contoh seperti ini mengkombinasikan kecepatan tinggi DES dengan kepercayaan pengelolaan kunci dengan sistem RSA. 

7. Contoh Kasus Algoritma RSA Untuk Pembuktian dan Penandaan Digital dalam praktiknya Sistem kriptografi kunci publik RSA bisa digunakan untuk membuktikan dan mengenali orang lain atau sesuatu yang memang ada. Alasan mengapa RSA bisa digunakan adalah setiap hal yang memang benar memiiki kunci privat yang berhubungan yang (secara teori) tidak ada orang lain yang dapat menembusnya. Hal ini berguna untuk identifikasi positif dan unik. Contohnya, umpamanya Fatma hendak mengirimkan pesan kepada Agus. Dia menggunakan fungsi hash terhadap pesan untuk menciptakan inti dari pesan, yang disediakan sebagai ”cap jari digital ” dari pesan tersebut.  Kemudian Fatma mengenkripsikan inti dari pesan tersebut dengan kunci privat miliknya, membuat tanda digital untuk kemudian dikirim kepada Agus bersamaan dengan pesannnya sendiri. Agus, setelah menerima pesan dan tanda, mengdekripsikan tanda dengan kunci public milik Fatma untuk medapatkan kembali inti dari pesan tersebut. Kemudian Agus mengubah kembali pesan dengan fungsi hash yang sama dengan yang dipakai oleh Fatma dan membandingkan hasilnya dengan inti dari pesan yang telah didekripsikan dari tanda.  Jika keduanya secara tepat sama, tanda tadi telah berhasi diverifikasi dan Agus dapat meyakini bahwa pesan tersebut benar-benar dari Fatma. Jika ternyata keduanya tidak tepat sama, entah pesan tersebut memang seperti itu atau telah diubah setelah ditandai, Agus dapat menolak pesan tersebut. Siapapun yang membaca pesan ini dapat menguji tandanya. Hal ini tidak dapat memuaskan keadaan dimana Fatma hendak mempertahankan kerahasiaan dokumen tersebut. Dalam keadaan seperti ini dia mungkin hendak menandai dokumen tersebut kemudian mengenkripsinya dengan kunci publik milik Agus. Agus kemudian harus mengdekripsikan dokumen tersebut dengan kunci publiknya dan memeriksa tanda pada pesan yang telah didapatkan kembali menggunakan kunci public milik Fatma.  Cara lain, jika dibutuhkan untuk memiliki pihak ketiga untuk mensahkan kesahan dari pesan tanpa dapat mengdekripsikan pesan, daripada dalam bentuk plainteks. Dalam praktiknya, eksponen publik dalam algoritma RSA bisaanya jauh lebih kecil dari

eksponen privat. Hal ini bermakna bahwa pembuktian tanda lebih cepat daripada penandaan. Hal seperti ini diinginkan karena sebuah pesan akan ditandai oleh seseorang hanya untuk satu kali, tetapi tanda yang terdapat pada pesan tersebut mungkin akan diuji beberapa kali oleh beberapa orang. Haruslah menjadi suatu hal yang tidak mungkin bagi seseorang baik untuk mendapatkan sebuah pesan yang diubah dengan suatu fungsi hash menjadi sebuah nilai yang telah diberikan maupun untuk mendapatkan dua buah pesan yang diubah menjadi nilai yang sama. Jika memang mungkin terjadi, seorang pengacau bisa melampirkan sebuah pesan yang salah pada tanda yang telah diberikan oleh Fatma.  Fungsi-fungsi hash seperti MD5 dan SHA telah dirancang secara khusus untuk mempunyai suatu sifat bahwa suatu kesamaan adalah hal yang tidak mungkin terjadi, dan oleh karena itu benarbenar dipertimbangkan sesuai dengan penggunaan dalam kriptografi. Satu atau lebih sertifikat bisa menyertai sebuah tanda digital. Sebuah sertifikat adalah sebuah dokumen yang telah ditandai yang mengikat kunci publik pada suatu identitas dari sebuah kelompok. Tujuannya adalah untuk menghalangi seseorang menirukan seseorang yang lain. Jika sebuah sertifikat adalah kata-kata, orang yang menerima (atau suatu pihak ketiga) bisa memeriksa bahwa kunci publik tersebut merupakan milik dari suatu kelompok yang telah dinamai, anggap orang yang menandai kunci publik sudah dapat dipercayai. 

8. Penggunaan RSA Sistem RSA sekarang digunakan oleh berbagai macam jenis produk, platform, dan industri di seluruh bagian dunia. Algoritma RSA digunakan dalam banyak perangkat lunak yang dijual secara komersial dan direncanakan akan digunakan pada banyak perangkat lunak lainnya. Algoritma RSA terpasang dalam sistem operasi pada hari ini oleh Microsoft, Apple, Sun, dan Novell. Berbicara tentang perangkat keras, algoritma RSA juga dapat ditemukan pemanfaatannya dalam telefon yang aman, dalam kartu-kartu jaringan Ethernet, dan dalam kartu-kartu cerdas (smart cards). Sebagai tambahan, algoritma RSA tergabung ke dalam semua protokol-protokol utama untuk komunikasi internet yang koko, termasuk S/MIME, SSL, dan S/WAN.  Algoritma RSA juga dimanfaatkan secara internal oleh banyak lembaga, termasuk cabangcabang dari Pemerintah Amerika Serikat (AS), badanbadan hukum utama, perpustakaan-perpustakaan nasional dan universitas-universitas. Pada saat penerbitan algoritma RSA, teknologi yang menggunakan algoritma RSA didaftarkan lebih dari 700 perusahaan. Teknologi enkripsi berbasis RSA BSAFE yang dipasang diperkirakan mencapai angka 500 juta. Kebanyakan dari penerapan-penerapan ini mencakup penggunaan algoritma RSA, membuat algoritma RSA secara signifikan merupakan system

kriptografi yang penggunaannya paling luas di dunia. Hal ini diperkirakan akan semakin bertambah besar dengan sangat cepat karena penggunaan Internet dan World Wide Web semakin bertambah luas. 

9. RSA Sebagai Standar Resmi Sistem kriptografi dengan menggunakan algoritma RSA merupakan bagian dari banyak standar resmi di seluruh dunia. Standar ISO (International Standards Organization) 9796 mencantumkan RSA sebagai algoritma kriptografi yang cocok, begitu juga dengan standar keamanan ITU-TX. 509. Sistem RSA adalah bagian dari standar Society for Worldwide Interbank Financial Telecommunications (SWIFT), standar rench financial industry's ETEBAC 5, standar ANSI X9. 31 rDSA dan naskah standar X9. 44 untuk industri perbankan Amerika Serikat.  RSA juga dicantumkan dalam standar pengelolaan kunci Australia, AS2805. 6. 5. 3. Algoritma RSA dapat ditemukan dalam standarstandar internet dan protokol-protokol yang dianjurkan, termasuk S/MIME, IPSec, dan TLS (penerus dari standar internet SSL), demikian juga dalam standar PKCS untuk penggunaan dalam perangkat lunak. OSI Implementers' Workshop (OIW) mengeluarkan perjanjian pemakai berkenaan dengan PKCS, yang mencakup penggaunaan RSA.  Sejumlah standar-standar lainnya sekarang sedang dikembangkan dan akan diumumkan dalam beberapa tahun mendatang. Beberapa di antaranya kemungkinan besar akan mencakup penggunaan algoritma RSA baik sebagai sistem yang sah atau yang dianjurkan dalam kerahasiaan dan/atau penandaan. Sebagai contoh, IEEE P1363 dan WAP WTLS mencakup penggunaan sistem RSA. 

10. RSA Sebagai Standar Yang De Facto Sistem RSA sudah digunakan begitu luas dalam sistem kriptografi kunci publik belakangan ini dan sering disebut sebagai standar yang de facto. Tanpa memperhatikan standar-standar resmi, keberadaan standar de facto sangat penting untuk pengembangan ekonomi digital. Jika satu sistem kunci publik digunakan dimana saja untuk pembuktian keaslian, kemudian dokumen digital yang telah ditandai dapat ditukarkan antara useruser yang berada pada negara-negara yang berbeda menggunakan perangkat lunak yang berbeda pada platform-platform yang berbeda; kemampuan antar operator ini penting untuk sebuah perkembangan bagi ekonomi digital yang nyata.  Pemakaian sistem RSA telah berkembang begitu luas sehingga dibutuhkan standar untuk memfasilitasinya. Ketika sebuah penjaja (vendor) industri perbankan AS yang maju mengembangkan standar-standar untuk penandaan digital, perusahaan ini mengembangkan ANSI X9. 30 pada tahun 1997 untuk mendukung syarat negara untuk penggunaan

standar penandaan digital (Digital Signature Standard). Satu tahun kemudian perusahaan ini menambahkan ANSI X9. 31, yang menekankan penandaan digital RSA untuk mendukung standar de facto dalam lembaga perbankan.   Kurangnya keamanan dalam membuktikan keaslian telah menjadi penghalang utama dalam usaha untuk mewujudkan impian bahwa komputer akan dapat menggantikan kertas. Kertas tetap menjadi sangat penting dimanapun untuk kontrak-kontrak, cek, surat resmi, dokumen legal dan pengenalan. Dengan berinti pada kebutuhan akan transaksi kertas ini, masih merupakan hal yang tidak mungkin untuk berkembang secara keseluruhan menuju masyarakat yang berbasis pada transaksi elektronik.  Tanda-tanda digital memungkinkan passport, transkrip kuliah, surat wasiat, kontrak sewa, cek, dan pendaftaran pemilih dalam bentuk elektronik. Bentuk kertas hanya sebuah salinan dari aslinya berupa dokumen elektronik. Standar yand telah diterima untuk penandaan digital memungkinkan semua hal ini terjadi. 

Algoritma RSA

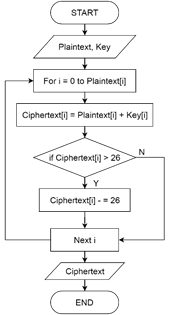
CODINGAN ALGORITMA RSA

package ksl;

import java.math.BigInteger;

import java.util.Random;

public class ksk {

    private BigInteger p;

    private BigInteger q;

    private BigInteger n;

    private BigInteger eulertot;

    private BigInteger e;

    private BigInteger d;

    private int panjangbit = 1024;

    private int ukuran_kunci_sandi = 256;

    private Random random;

   

    public ksk (){

        random = new Random();

        p = BigInteger.probablePrime(panjangbit, random);

        q = BigInteger.probablePrime(panjangbit, random);

        n = p.multiply(q);

        eulertot = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE));

        e = BigInteger.probablePrime(panjangbit/2, random);

        while (eulertot.gcd(e).compareTo(BigInteger.ONE)>0&& e.compareTo(eulertot)<0){

            e.add(BigInteger.ONE);

        }

        d = e.modInverse(eulertot);

    }

    public byte [] enkripsi (byte [] data){

       return (new BigInteger(data)).modPow(e, n).toByteArray();

    }

    public byte [] deskrip(byte [] data){

        return (new BigInteger(data)).modPow(d, n).toByteArray();

    }

    private static String byte_ke_String(byte [] data){

        String hasil = "";

        for (byte b : data){

            hasil += Byte.toString(b);

        }

        return hasil;

    }

    public static void main(String[] args){

        String pesan = "dicky fajar NIM 201631149";

        ksk rsa = new ksk();

        System.out.println("pesan asli = "+pesan);

        byte[] hasilRSA = rsa.enkripsi(pesan.getBytes());

       

        System.out.println("hasil enkripsi = "+byte_ke_String(hasilRSA));

        byte[] hasilDe = rsa.deskrip(hasilRSA);

        System.out.println("hasil dekrip RSA string byte = "+byte_ke_String(hasilDe));

        Syst

em.out.println("hasil  = "+new String(hasilDe));

        }

       

    }